4.Приближенное дифференцирование

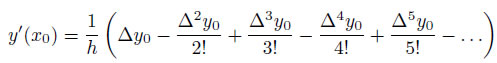
Идея численного дифференцирования заключается в том, что функцию y(x), заданную в равноотстоящих точках x_i (i = 0, 1, . . . , n) отрезка [a, b] с помощью значений y_i = f(x_i), приближенно заменяют интерполяционным полиномом Ньютона, построенном для системы узлов x₀, x₁, . . . , x_k (k меньше или равно n), и вычисляют производные y′ = f′(x), y′′ = f′′(x) и т. д.

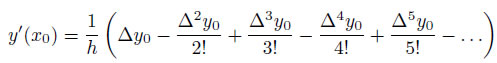
На практике приближенное дифференцирование применяют в основном для функций, заданных в виде таблицы. В Scilab численное дифференцирование реализовано командой

dy=diff(y,n)

где y – значения функции y(x) в виде вектора вещественных чисел,
n – порядок дифференцирования.

Результат работы функции – вектор вещественных чисел dy, представляющий собой разности порядка n и интерполяционного полинома Ньютона . Рассмотрим работу функции на примере:

Решение данной задачи: