В Scilab численное интегрирование по методу трапеций реализовано с помощью функции
inttrap(x,y)
Эта функция вычисляет площадь фигуры под графиком функции y(x), которая описана набором точек (x, y). Параметр x является необязательным. Для функции inttrap(y) элементы вектора x принимают значения номеров элементов вектора y.
Этот интеграл легко сводится к табличному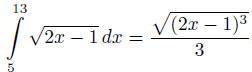 
, поэтому вычислить его можно вычислить по формуле Ньютона–Лейбница:
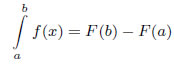
В Scilab это будет выглядеть следующим образом:
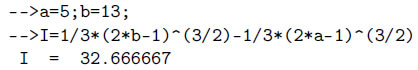
Теперь применим для отыскания заданного определенного интеграла метод трапеций, суть которого состоит в следующем: для вычисления интеграла методом трапеций участок интегрирования разбивают на определенное количество равных отрезков, каждую из полученных криволинейных трапеций заменяют прямолинейной и вычисляют приближенное значение интеграла как сумму площадей этих трапеций.
Рассмотрим несколько вариантов решения данной задачи. В первом случае интервал интегрирования делится на отрезки с шагом 1, во втором 0.5 и в третьем 0.1. Не трудно заметить, что чем больше точек разбиения, тем точнее значение искомого интеграла:
Далее приведен пример использования функции inttrap с одним аргументом:
Как видим, в первом случае значение интеграла, вычисленного при помощи этой функции, неточно и совпадает со значением, полученным функцией inttrap(x,y) на интервале [5; 13] с шагом 1. Т.е. мы нашли сумму площадей восьми прямолинейных трапеций с основанием h = 1 и боковыми сторонами, заданными вектором y.
Во втором случае, при попытке увеличить точность интегрирования, значение интеграла существенно увеличивается. Дело в том, что, уменьшив шаг разбиения интервала интегрирования до 0.1, мы увеличили количество элементов векторов x и y, и применение функции inttrap(y) приведет к вычислению суммы площадей восьмидесяти трапеций с основанием h = 1 и боковыми сторонами, заданными вектором y. Таким образом, в первом и втором примерах вычисляются площади совершенно разных фигур.
| Назад | Содержание | Далее |