3. Решение задач линейного программирования

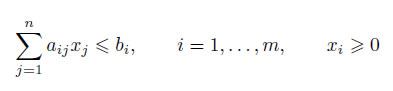
В общем случае задачу линейного программирования можно сформулировать следующим образом. Найти такие значения x₁, x₂, . . . , x_n, удовлетворяющие системе ограничений

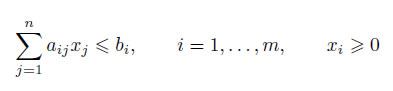
, при которых функция цели L

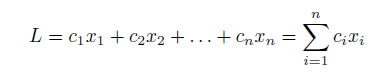
достигает своего минимального (максимального) значения.

Для решения задач линейного программирования предназначена функция linpro следующей структуры:

[x,kl,f]=linpro(с,A,b[,ci,cs][,k][,x0])

Здесь:

c – массив (вектор-столбец) коэффициентов при неизвестных функции цели, длина вектора n совпадает с количеством неизвестных x.

A – матрица при неизвестных из левой части системы ограничений, количество строк матрицы равно количеству ограничений m, а количество столбцов совпадает с количеством неизвестных n.

b – массив (вектор-столбец), содержит свободные члены системы ограничений, длина вектора m.

ci – массив (вектор-столбец) размерности n содержит нижнюю границу переменных ; если таковая отсутствует, указывают [ ].

cs – массив (вектор-столбец) длиной n, содержит верхнюю границу переменных ; если таковая отсутствует, указывают [ ].

k – целочисленная переменная, используется, если в систему ограничений кроме неравенств входят и равенства, в матрице они будут находиться в k первых строках, оставшиеся l строк займут неравенства,
т.е. m = k + l.

x0 – вектор-столбец начальных приближений длиной n.

Функция linpro возвращает массив неизвестных x, минимальное значение функции f и массив множителей Лагранжа kl.

Рассмотрим использование функции linpro на примере решения следующей задачи линейного программирования.

Обратите внимание, что в четвертом ограничении присутствует знак больше-равно. Для приведения системы ограничений к необходимому виду 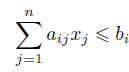необходимо четвертое уравнение умножить на -1. Решение задачи представлено ниже:

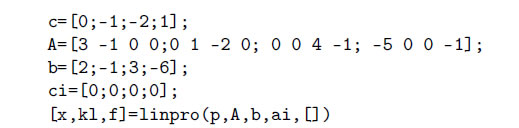
Результаты решения задачи, которые появятся в главном окне: