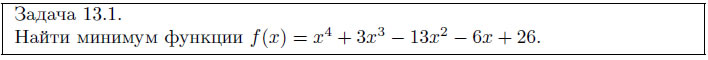
В качестве простейшей оптимизационной задачи рассмотрим поиск локального минимума функции одной переменной.
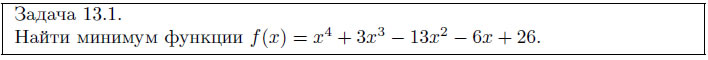
Решение задачи начнем с построения графика функции:
График:
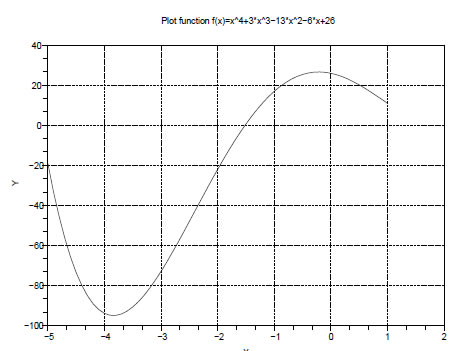
Из графика видно, что функция имеет минимум в районе точки -4. Для нахождения более точного значения минимума функции в Scilab служит функция
[f,xopt]=optim(costf,x0)
,которая предназначена для поиска минимума любой функции, x0 – вектор-столбец начальных приближений длиной n, функция costf определяет функцию, минимум которой ищется. Функция возвращает минимум функции (f) и точку, в которой функция достигает этого значения (xopt). Главной особенностью функции optim является структура функции costf, которая должна быть следующей:

Для функции одной переменной в качестве f возвращается функция, минимум которой ищется, в качестве функции g – ее производная.
Если возвращаемое сформированной функцией costf значение ind равно 2, 3 или 4, то функция costf обеспечивает поиск минимума, т. е. в качестве результата функции optim возвращается f и xopt. Если ind=1, то в функциии optim ничего не считается, условие ind<0 означает, что минимум f(x) не может быть оценен, а ind=0 прерывает оптимизацию.
Вообще говоря, значение параметра ind является внутренним параметром для связи между optim и costf, для использования optim необходимо помнить, что параметр ind должен быть определен в функции costf.
Таким образом, при использовании функции optim необходимо сформировать функцию costf, которая должна возвращать минимизируемую функцию f и ее градиент (производную).
Рассмотрим использование функции optim для поиска минимума функции (см. Задание 13.1):

Ниже представлен результат поиска минимума функции одной переменной:

Аналогично можно найти минимум любой другой функции одной переменной, главной задачей является проблема правильного выбора точки начального приближения. Но это проблема не пакета Scilab, а математическая проблема.
| Назад | Содержание | Далее |