Простейшая задача интерполирования заключается в следующем. На отрезке [a; b] заданы
точки x0, x1, x2, . . . , xn (всего n+1 точка), которые называют узлами интерполяции, и значения некоторой функции f(x) в этих точках:
![]()
Требуется построить интерполирующую функцию F(x), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и f(x):
![]()
Для решения подобной задачи довольно часто используют сплайн-интерполяцию (от английского слова spline – рейка, линейка). Один из наиболее распространенных вариантов интерполяции – интерполяция кубическими сплайнами. Кроме того, существуют квадратичные и линейные сплайны.
В Scilab для построения линейной интерполяции служит функция:
y=interpln(z,x)
где z – матрица исходных драных; x – вектор абсцисс; y – вектор значений линейного сплайна в точка x.
Далее приведен пример использования функции interpln. Здесь линейный сплайн применяется для решения знакомой задачи 11.1 из первого раздела (метод наименьших квадратов):
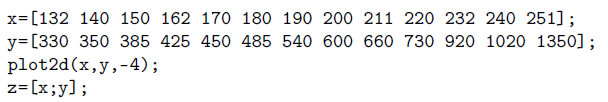
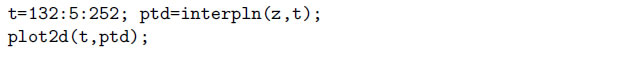
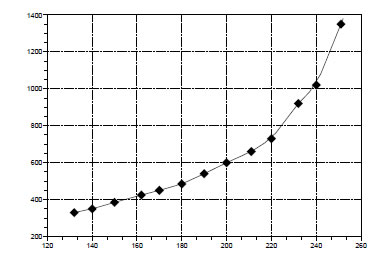
Графическое решение задачи показано на рисунке.
| Назад | Содержание | Далее |