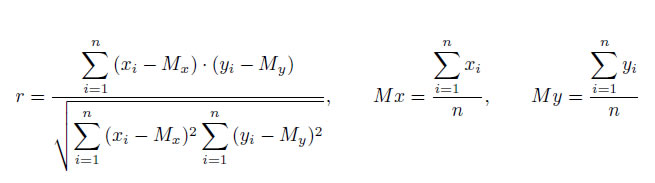
Одной из наиболее часто используемых в методе наименьших квадратов функций является прямая, описываемая уравнением вида y = a1 + a2x, которая называется линией регрессии y на x. Параметры a1 и a2 являются коэффициентами регрессии. Показатель, характеризующий тесноту линейной связи между x и y, называемый коэффициентом корреляции, рассчитывается по формуле:
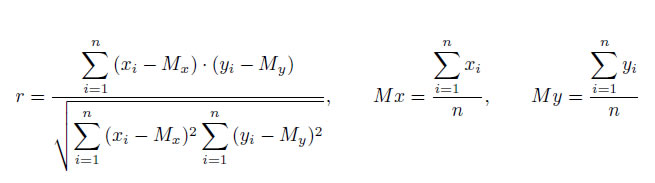
Значение коэффициента корреляции удовлетворяет соотношению 
. Чем меньше отличается абсолютная величина r от единицы, тем ближе к линии регрессии располагаются экспериментальные точки. Если коэффициент корреляции близок к нулю, то это означает, что между x и y отсутствует линейная связь, но может существовать другая, нелинейная, зависимость. Аналогом коэффициента корреляции r для нелинейных зависимостей является индекс корреляции, рассчитываемый по формуле:
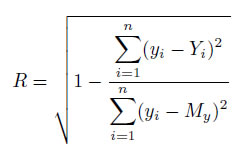
где y – экспериментальные значения, Y – значения, найденные методом наименьших квадратов, My – среднее значение y. Индекс корреляции по своему абсолютному значению колеблется в пределах от 0 до 1. При функциональной зависимости индекс корреляции равен 1. В случае отсутствии связи R = 0. Если коэффициент корреляции r является мерой тесноты связи только для линейной формы, то индекс корреляции R – и для линейной, и для криволинейной. При прямолинейной связи коэффициент корреляции по своей абсолютной величине равен индексу корреляции.
Для расчета коэффициентов регрессии предназначена функция:
a=regress(x,y)
где x и y – экспериментальные данные, a – вектор коэффициентов линии регрессии a1 и a2.
Рассмотрим работу этой функции на примере:
Данные о растворимости NaNO3 в зависимости от температуры воды:
Решение задачи:
Построение графика экспериментальных данных и линии регрессии:
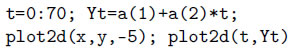
Графическое решение задачи:
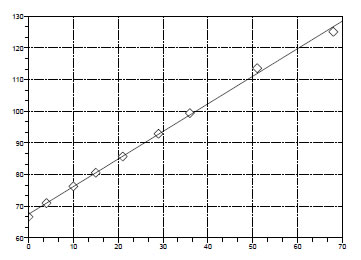
Для расчета коэффициента корреляции в Scilab также предназначена встроенная функция a=corr(x,y), где x и y –– экспериментальные данные.
| Назад | Содержание | Далее |