1.Метод наименьших квадратов

Метод наименьших квадратов позволяет по экспериментальным данным подобрать такую аналитическую функцию, которая проходит настолько близко к экспериментальным точкам, насколько это возможно.

Пусть в результате эксперимента были получены некоторые данные, отображенные в виде таблицы. Требуется построить аналитическую зависимость, наиболее точно описывающую результаты эксперимента.

Идея метода наименьших квадратов заключается в том, что функцию Y =f(x, a₀, a₁, . . . , a_k) необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений y_i от расчетных Y_i была наименьшей:

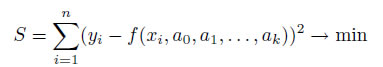
Задача сводится к определению коэффициентов a_i. Для реализации этой задачи в Scilab предусмотрена функция
[a,S]=datafit(F,z,с)

где F – функция, параметры которой необходимо подобрать; z – матрица исходных данных; c – вектор начальных приближений; a – вектор коэффициентов; S – сумма квадратов отклонений измеренных значений от расчетных.

Рассмотрим использование функции datafit на примере:

Зависимость потребляемой из сети мощности от входного напряжения:

Методом наименьших квадратов подобрать зависимость вида P = a₁ +a₂U +a₃U² + a₄U³.
Далее приведено решение задачи с комментариями:

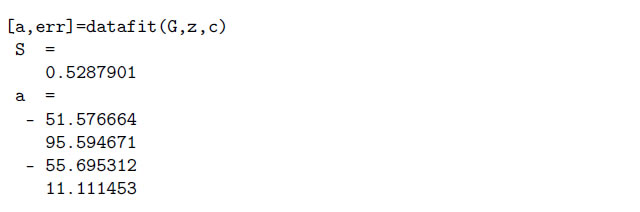
Итак, в результате работы функции datafit была подобрана аналитическая зависимость
вида , а сумма квадратов отклонений измеренных значений от расчетных составила 0.529.

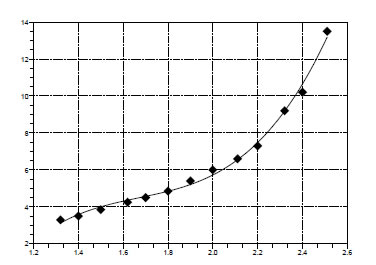
Построение графика подобранной зависимости:

Графическая интерпретация задачи: