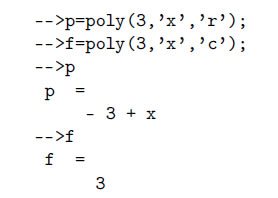
Любое уравнение P(x) = 0, где P(x) – это многочлен, отличный от нулевого, называется алгебраическим уравнением или полиномом. Всякое алгебраическое уравнение относительно x можно записать в виде
a0xn+a1xn-1+· · ·+an-1x+an = 0
, где a0 не равно 0, n > 1 и ai – коэффициенты алгебраического уравнения n–й степени.
Например, линейное уравнение это алгебраическое уравнение первой степени, квадратное – второй, кубическое – третьей и так далее.
Решение алгебраического уравнения в Scilab состоит из двух этапов. Необходимо задать полином P(x) с помощью функции poly, а затем найти его корни, применив функцию roots.
Итак, определение полиномов в Scilab осуществляет функция:
poly(a, "x", [" F"])
где a – это число или матрица чисел, x – символьная переменная, F – необязательная символьная переменная, определяющая способ задания полинома. Символьная переменная F может принимать только два значения – roots или coeff (соответственно r или c).
Если F=c, то будет сформирован полином с коэффициентами, хранящимися в параметре a. Если же F=r, то значения параметра a воспринимаются функцией как корни, для которых необходимо рассчитать коэффициенты соответствующего полинома. По умолчанию F=r.
Следующий пример отражает создание полинома p, имеющего в качестве корня тройку, и полинома f с коэффициентом 3:
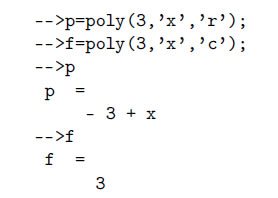
Далее приведены примеры создания более сложных полиномов:

C полиномами возможно проведение символьных операций, таких как: сложение, вычитание, умножение, деление, возведение в степень. Например:
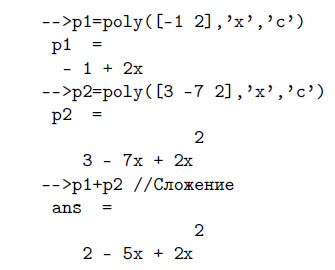
| Назад | Содержание | Далее |