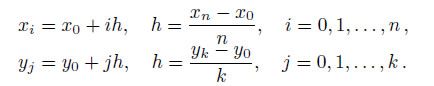
К трехмерным отнесем все графики, положение каждой точки которых задается тремя величинами.
В целом процесс построения графика функции вида Z(x, y) можно разделить на три этапа:
1. Создание в области построения графика прямоугольной сетки. Для этого формируются прямые линии, параллельные координатным осям xi и yj , где
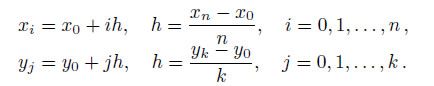
2. Вычисление значений функции zij = f(xi, yj) во всех узлах сетки.
3. Обращение к функции построения трехмерных графиков.
В Scilab поверхность можно построить с помощью функций plot3d . Обращение к функциям следующее:
plot3d(x,y,z)
здесь x – вектор-столбец значений абсцисс; y – вектор-столбец значений ординат; z – матрица значений функции;
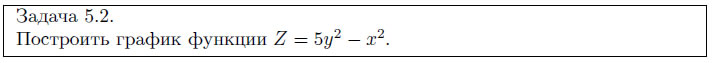
Прежде всего зададим массивы X и Y . Затем сформируем матрицу значений функции Zij (xi, yj), используя оператор цикла for. Здесь i – параметр цикла, который будет перебирать все значения массива X, а
j – параметр цикла, который будет сопоставлять каждому значению массива X по очереди все значения
массива Y .
Таким образом, сначала будут вычислены все значения функции Z при меняющемся Y (от первого до последнего значения в массиве) и первом значении массива X. Затем – при втором значении массива X
и т. д. Напомним, здесь length – определяет количество элементов массива X или Y. Наконец, для построения поверхности обратимся к функции plot3d1 (аналог функции plot3d). Их отличие состоит в том, что plot3d строит поверхность и заливает ее одним цветом, а plot3d1 – поверхность, каждая ячейка которой имеет цвет, зависящий от значения функции в каждом соответствующем узле сетки.
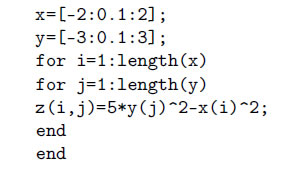
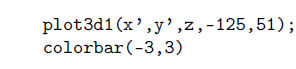
Функция plot3d2 и является аналогом функции plot3d (не путать функции plot3d-plot3d1-plot3d2), поэтому имеет такой же синтаксис:
plot3d2(x,y,z,)
Эти функции предназначены для построения поверхности, которая задается набором граней. Т. е. если функция plot3d по входным данным сможет построить лишь отдельно стоящие друг от друга плоские грани, то plot3d2 проинтерпретирует взаимное расположение этих граней в виде цельного геометрического тела.
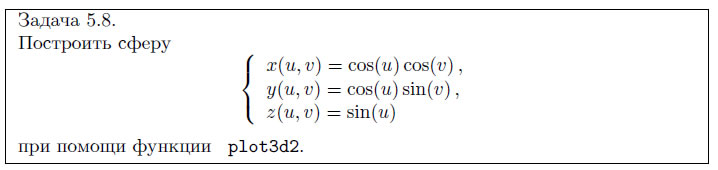
При построении графиков поверхностей, заданных параметрически – x(u, v), y(u, v)и z(u, v) – необходимо сформировать матрицы X, Y и Z одинакового размера. Для этого массивы u и v должны иметь одинаковый размер. После этого
1. Если x, y и z можно представить в виде произведения f(u) · g(v), то соответствующие X, Y и Z следует формировать в виде матричного умножения f(u) на g(v).
2. Если x, y и z можно представить в виде одной функции f(u) или g(v), то в этом случае матрицы X, Y и Z следует записывать в виде f(u) · ones(size(v)) или g(v) · ones(size(u)) соответственно.
Отметим также, что здесь linspace – функция, возвращающая массив с линейным приращением значений в заданном диапазоне. Например, u=linspace(-%pi/2,%pi/2,40) значит, что параметр u линейно изменяется в диапазоне [−2π; 2π]. Число 40 устанавливает, что массив должен содержать ровно 40 значений, по умолчанию их 100.

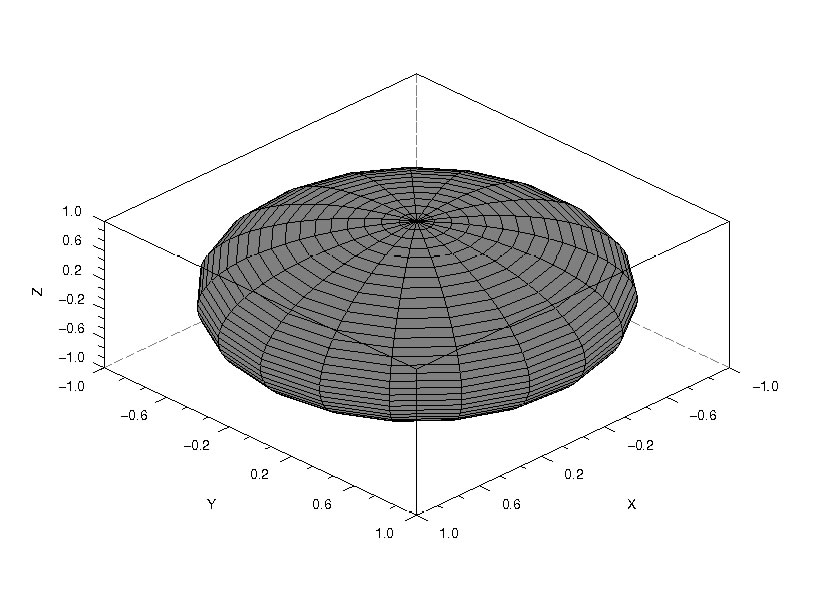
Построенная функцией plot3d2 сфера представлена ниже:
| Назад | Содержание | Далее |