4.Решение систем линейных алгебраических уравнений

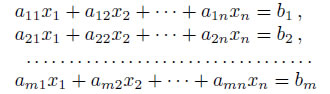
Система m уравнений с n неизвестными вида:

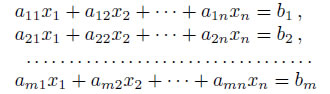
Система из m линейных уравнений с n неизвестными может быть описана при помощи матриц: A · x = b, где x — вектор неизвестных, A —матрица коэффициентов при неизвестных или матрица системы,
b — вектор свободных членов системы или вектор правых частей.

Совокупность всех решений системы (x₁, x₂, . . . , x_n) называется множеством решений или просто решением системы.

Существует несколько способов решения систем уравнений:

Метод Крамера

Правило Крамера заключается в следующем. Если определительматрицы системы из n уравнений с n неизвестными A· x = b отличен от нуля, то система имеет единственное решение x₁, x₂, . . . , x_n, определяемое по формулам Крамера: , где — определитель матрицы, полученной из матрицы системы A заменой i-го столбца столбцом свободных членов b.

Метод обратной матрицы

Для системы из n линейных уравнений с n неизвестными A · x = b, при условии, что определитель матрицы A не равен нулю, единственное решение можно представить в виде x = A⁻¹ · b.

Метод Гаусса

Решение системы линейных уравнений при помощи метода Гаусса основывается на том, что от заданной системы переходят к эквивалентной системе, которая решается проще, чем исходная система.

Метод Гаусса состоит из двух этапов. Первый этап — это прямой ход, в результате которого расширенная матрица системы путем элементарных преобразований (перестановка уравнений системы, умножение уравнений на число, отличное от нуля, и сложение уравнений) приводится к ступенчатому виду. На втором этапе (обратный ход) ступенчатую матрицу преобразовывают так, чтобы в первых n столбцах получилась единичная матрица. Последний, n + 1 столбец этой матрицы содержит решение системы линейных уравнений.